Recursive Factorial Computation

The factorial of n or n! is computed as follows:

   0!=1

   n!=n x (n - 1)!

The first formula tells us about the base case: n equal to 0. The second formula is a recursive definition.It leads to the following algorithm for computing n! recursively.

Factorial(n)
if n = 0
n! = 1
else
n!=n x (n - 1)!

To verify the correctness of the algorithm, we see that the base case is solved correctly (0! is 1).The recursive case makes progress towards the base case because it involves the calculation of a smaller factorial. Also,if we can calculate (n - 1)!, the recursive case gives us the correct formula for calculating n!

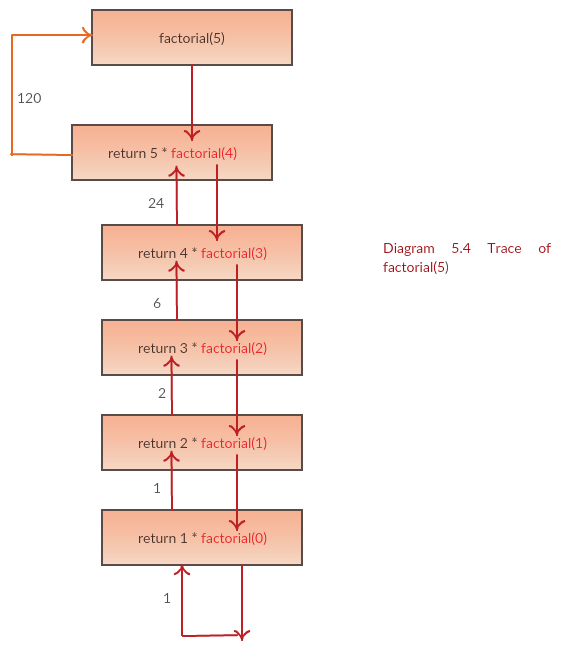
The recursive method follows.The statement return n* factorial (n - 1); implements the recursive case.Each time factorial calls itself, the method body executes again with a different argument value. Factorial(5) will generate five recursive calls as shown in the below diagram.

JAVA IMPLEMENTATION

import java.util.Scanner;

/**
 * Created by Ganesh.r.hegde on 16-Feb-18.
 */
public class Factorial {


    public static void main(String[] args) {

        Scanner scan = new Scanner(System.in);
        System.out.println("Enter the integer who factorial is needed : ");

        int number = scan.nextInt();

        if(number > 31)
            throw new StackOverflowError("Number cannot exceed 31");
        else
           System.out.println("The factorial of "+number +" is "+factorial(number));

    }


    /** Recursive factorial method
     pre: n >= 0
     @param n The integer whose factorial is being computed
     @return n!
     */
    public static int factorial(int n) {

        if( n < 0)
            throw new ArithmeticException("Negative integer not allowed in factorial computation");
        else
        if (n == 0)
            return 1;
        else
            return n * factorial( n - 1);
    }
}